|
DOI: 10.7256/2454-0714.2021.2.36014
Received:
25-06-2021
Published:
02-07-2021
Abstract:
This article examines the model of pursuit task, when the pursuer while moving in space, adheres to the strategy of constant-bearing approach. The velocity modules of the pursuer and target are constant. The object moves evenly and straightforwardly, for certainty of the model, since the test program is written based on the materials of the article. The velocity vectors of the target and the pursuer in the beginning of the pursuit are directed arbitrarily. The iterative process consists of the three parts. Calculation of trajectory of the pursuer in space, calculation of trajectory of the pursuer in a plane, calculation of the transition of trajectory from space to a plane are conducted. All parts of the iterative process have to meet the conditions specified in a task. An important condition is that the minimum radius of curvature of the trajectory should not exceed a certain set value. The scientific novelty of the geometric model consists in the possibility to regulate the time of reaching the target by changing the length of trajectory of the pursuer, as well as the orientation of a plane of pursuit. Calculation of the point of next position of the pursuer in space is the point of intersection of the sphere, cone and plane of constant-bearing approach. A plane of constant-bearing approach is perpendicular to a plane of pursuit. In the model under review, a plane of pursuit is determined by the target velocity vector and direct target that connects the pursuer and the target (sight line). The radius of the sphere is equal to the step of the pursuer for the time interval the time of the iterative process is divided into. The angle of solution of the cone is the angle by which the velocity vector of the pursuer can turn. The mathematical model presented in the article may be of interest to developers of unmanned aerial vehicles.
Keywords:
Persuit, Pursuer, Target, Curvature, Line, Trajectory, Cone, Attainment, Parallel, Plane
This article written in Russian. You can find original text of the article here
.
I. Введение
В методе расчета траектории преследователя на плоскости вектор скорости преследователя в точку на окружности Аполлония.
|

|
|
Рис.1 – Окружность Аполлония
|
На рисунке 1 точка 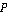 - это положение преследователя, а точка - это положение преследователя, а точка 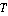 - это положение цели. Окружностью Аполлония называется множество точек - это положение цели. Окружностью Аполлония называется множество точек  , для которых характерно то, что отношение расстояний до двух фиксированных точек (точки , для которых характерно то, что отношение расстояний до двух фиксированных точек (точки 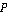 и и 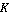 на рисунке 1). на рисунке 1).
Применительно к задаче преследования это будет выглядеть так:
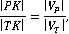
где 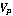 - это скорость преследователя, - это скорость преследователя, 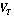 – скорость цели. Фиксированное направление движения цели выделяет на окружности Аполлония единственную точку – скорость цели. Фиксированное направление движения цели выделяет на окружности Аполлония единственную точку 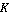 и единственное направление скорости и единственное направление скорости 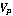 преследователя. преследователя.
Тогда, для задачи преследования на плоскости, где преследователь и цель движутся прямолинейно и равномерно, имеет место быть итерационная схема, представленная на рисунке 2:
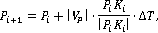
где 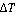 - это интервал времени дискретной задачи преследования. - это интервал времени дискретной задачи преследования.
Для случая, когда вектор скорости цели 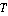 известен, то положение следующего шага цели известен, то положение следующего шага цели 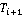 предопределено: предопределено:
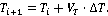
Координаты точки 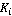 являются решением системы уравнений относительно параметра являются решением системы уравнений относительно параметра 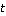 : :
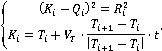
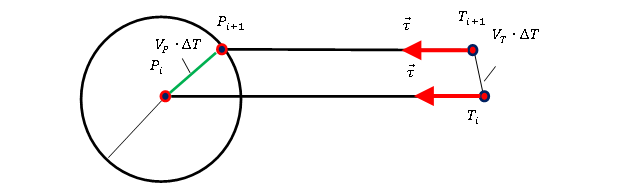
Радиус 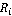 и центр окружности Аполлония и центр окружности Аполлония 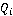 рассчитываются следующим образом: рассчитываются следующим образом:
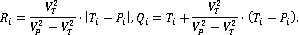
|
|
|
Рис.2 – Итерационная схема
|
Или, следуя итерационной схеме, изображенной на рисунке 2, шаг траектории преследователя 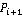 удовлетворяет решению системы уравнений (1), относительно параметра удовлетворяет решению системы уравнений (1), относительно параметра 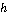 : :
|
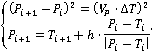
|
(1)
|
II. Постановка задачи
|
|
|
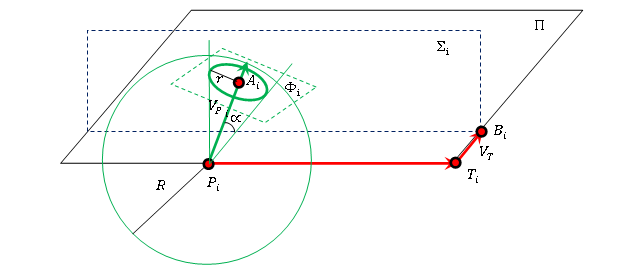
Рис. 3 – Итерационная схема в пространстве
|
Целью данной статьи является описание модели задачи преследования в пространстве, когда вектора скоростей преследователя и цели, на рисунке 3 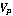 и и 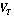 , соответственно, не лежат в одной плоскости. Задачей является расчет точек траектории преследователя при определенной траектории цели. , соответственно, не лежат в одной плоскости. Задачей является расчет точек траектории преследователя при определенной траектории цели.
Будем считать, что в любой момент времени движение цели можно представить, как прямолинейное и равномерное.
Плоскость, образованную линией визирования в момент начала преследования (на рисунке 3 это прямая 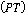 ) и вектором скорости ) и вектором скорости 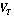 , будем считать координатной плоскостью , будем считать координатной плоскостью 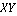 с началом в точке с началом в точке 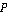 , осью абсцисс направленной вдоль прямой , осью абсцисс направленной вдоль прямой 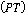 . .
Необходимо в итерационном процессе добиться того, чтобы координаты точки преследователя располагались в координатной плоскости 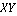 , на рисунке 3 это плоскость , на рисунке 3 это плоскость 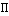 . При этом точка положения преследователя . При этом точка положения преследователя 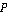 принадлежала соответственной моменту времени плоскости принадлежала соответственной моменту времени плоскости 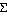 . Плоскость . Плоскость 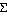 содержит следующий шаг цели (точка содержит следующий шаг цели (точка 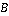 ), перпендикулярна плоскости ), перпендикулярна плоскости 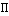 и параллельна линии визирования и параллельна линии визирования 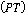 . .
Кроме того, траектория преследователя должна удовлетворять ограничениям на кривизну, то есть радиус кривизны траектории не может быть меньше некоторого порогового значения.
III. Теория
1. Расчет траектории преследователя в пространстве
В кинематической модели параллельного сближения в пространстве, рассматриваемой в данной статье траектория преследователя рассчитывается для двух случаев. В первом случае сегмент траектории расположен в пространстве. Во втором случае задача превращается в преследование на плоскости. Преследователь на рисунке 3 движется по плоскости 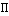 . Также рассчитывается плавный переход из пространства на плоскость. . Также рассчитывается плавный переход из пространства на плоскость.
Модель преследования является дискретной, поэтому вводится промежуток времени 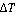 , за который участники итерационного процесса совершают шаг. Преследователь, находясь в точке , за который участники итерационного процесса совершают шаг. Преследователь, находясь в точке 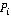 (Рис. 3), имеет возможность совершить шаг в пределах сферы радиуса (Рис. 3), имеет возможность совершить шаг в пределах сферы радиуса 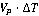 с центром в точке с центром в точке 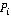 . . 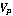 - модуль скорости равномерного движения преследователя. Это возможность ограничена правильным конусом с углом раствора - модуль скорости равномерного движения преследователя. Это возможность ограничена правильным конусом с углом раствора 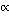 и вершиной в точке и вершиной в точке 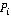 . .
Угол раствора конуса равен 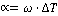 , , 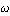 - максимальная частота углового вращения преследователя равная - максимальная частота углового вращения преследователя равная 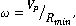 где где 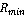 - минимальный радиус кривизны траектории преследователя. Кроме того, следующая точка - минимальный радиус кривизны траектории преследователя. Кроме того, следующая точка 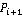 положения преследователя должна принадлежать плоскости положения преследователя должна принадлежать плоскости 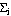 (Рис. 3). В дальнейшем, при переходе на плоскость (Рис. 3). В дальнейшем, при переходе на плоскость 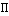 (Рис. 3), принадлежность к плоскости (Рис. 3), принадлежность к плоскости 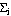 преобразуется в итерационную схему, представленную на рисунке 2. преобразуется в итерационную схему, представленную на рисунке 2.
Ось конуса направлена в направлении текущего вектора скорости 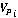 преследователя, выходящего из точки преследователя, выходящего из точки 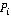 . Таким образом, имеется геометрическая задача расчета точки, принадлежащей трем поверхностям: сфере, конусу и плоскости. . Таким образом, имеется геометрическая задача расчета точки, принадлежащей трем поверхностям: сфере, конусу и плоскости.
Модель задачи преследования данной статьи позволяет произвести замену правильного конуса плоскостью. Линия пересечения правильного конуса и сферы принадлежит плоскости 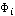 . Параметры плоскости . Параметры плоскости 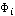 будут таковы: будут таковы: 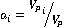 – единичный вектор нормали плоскости – единичный вектор нормали плоскости 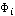 , вектор скорости для текущего положения преследователя , вектор скорости для текущего положения преследователя 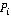 , , 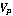 - модуль скорости равномерного движения преследователя, - модуль скорости равномерного движения преследователя, 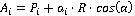 , где , где 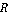 - радиус сферы, равный шагу преследователя - радиус сферы, равный шагу преследователя 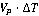 (Рис. 3). (Рис. 3).
Расчет точек пересечения плоскостей 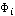 и и 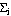 со сферой радиуса со сферой радиуса 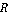 с центром в точке с центром в точке 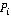 более предпочтителен, чем расчет точек пересечения сферы, конуса плоскости с точки зрения вычислительных трудностей. более предпочтителен, чем расчет точек пересечения сферы, конуса плоскости с точки зрения вычислительных трудностей.
У плоскости 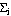 опорной точкой является точка опорной точкой является точка 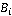 , нормалью является вектор , нормалью является вектор 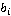 (Рис. 3): (Рис. 3):
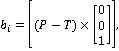
где 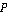 и и 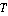 - начальные положения преследователя и цели. - начальные положения преследователя и цели.
В тестовой программе, написанной по материалам статьи, находится прямая (2), являющаяся пересечением плоскостей 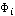 и и 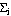 : :
|
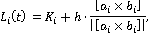
|
(2)
|
где 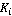 - точка пересечения плоскостей - точка пересечения плоскостей 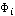 , , 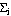 и и 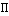 (рис. 3). (рис. 3).
Далее, выражаем точку 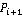 из первого уравнения системы (3) и подставляем его во второе уравнение системы (3): из первого уравнения системы (3) и подставляем его во второе уравнение системы (3):
|
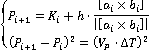
|
(3)
|
Найденное значение 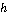 подставляем в первое уравнение системы (3), определив тем самым следующую точку подставляем в первое уравнение системы (3), определив тем самым следующую точку 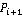 траектории преследователя. траектории преследователя.
Таким образом, итерационный процесс расчета траектории движения преследователя в пространстве можно считать сформированным.
2. Расчет траектории движения преследователя на плоскости
В случае перехода преследования на плоскость необходимо свести задачу к параллельному сближению, как это изображено на рисунке 1. В этом случае скорость преследователя всегда направлена в точку на окружности Аполлония (на рис. 1 это точка 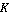 ). Тогда используется итерационная схема, представленная системой уравнений (1). ). Тогда используется итерационная схема, представленная системой уравнений (1).
Если скорость преследователя при переходе на плоскость направлена не на точку 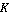 , как на рисунке 1, то при соблюдении некоторых условий по направлению движения преследователя, можно применить такую же итерационную схему, описанную системой уравнений (1). , как на рисунке 1, то при соблюдении некоторых условий по направлению движения преследователя, можно применить такую же итерационную схему, описанную системой уравнений (1).
|
|
|
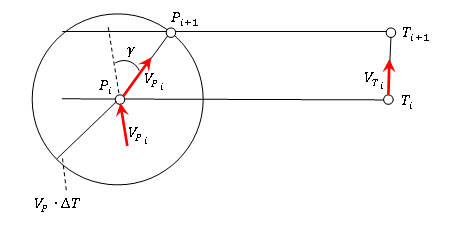
Рис. 4 – Дополнения к итерационной схеме
|
Условие по направлению движения заключается в следующем. Необходимо, чтобы угол 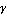 (Рис. 4) между скоростями (Рис. 4) между скоростями 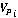 и и 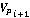 был меньше или равен угла был меньше или равен угла 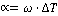 , где , где 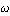 - допустимая скорость вращения преследователя, - допустимая скорость вращения преследователя, 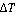 - временной промежуток итерационного процесса. - временной промежуток итерационного процесса.
Если угол 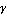 больше больше 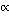 , но модуль скорости преследователя , но модуль скорости преследователя 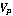 больше модуля скорости цели больше модуля скорости цели 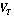 , то в качестве итерационной схемы можно предложить следующее (Рис. 5). , то в качестве итерационной схемы можно предложить следующее (Рис. 5).
|
|
|
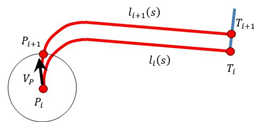
Рис. 5 Расчет следующего шага преследователя
|
В качестве однопараметрического множества параллельных линий визирования 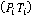 (Рис. 4) предложено множество составных параллельных линий (Рис. 4) предложено множество составных параллельных линий 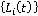 , которое формируется следующим образом: , которое формируется следующим образом: 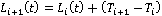 . Следующий шаг преследователя . Следующий шаг преследователя 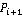 есть точка пересечения окружности радиуса есть точка пересечения окружности радиуса 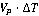 с центром в точке с центром в точке 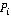 с линией с линией 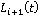 (Рис. 5). (Рис. 5).
Первая линия однопараметрического множества линий 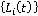 формируется из окружности минимального радиуса формируется из окружности минимального радиуса 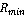 и прямой касательной линии, проходящей через точку и прямой касательной линии, проходящей через точку 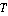 (Рис. 7). (Рис. 7).
На рисунке 7 показано взаимное расположение начальных положений преследователя и цели, вектора скорости преследователя 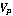 и указанной окружности. и указанной окружности.
|

|
|
Рис. 7 – Взаимное расположение преследователя, цели и окружности
|
На рисунке 7 показано, что центр указанной окружности находится в точке 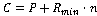 . Где . Где 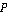 - это начальное положение преследователя, - это начальное положение преследователя, 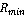 - минимальный радиус кривизны траектории преследователя, - минимальный радиус кривизны траектории преследователя, 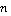 - единичный вектор, перпендикулярный вектору скорости преследователя - единичный вектор, перпендикулярный вектору скорости преследователя 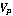 . Составная линия состоит из дуги . Составная линия состоит из дуги 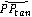 и прямолинейного сегмента и прямолинейного сегмента 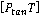 , где , где 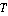 - это начальное положение цели, а - это начальное положение цели, а 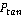 - точка касания с окружностью. - точка касания с окружностью.
3. Критерий перехода к плоскому движению
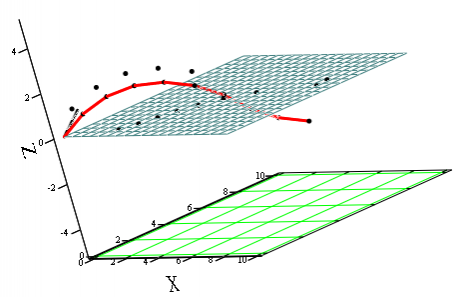
На рисунке 8 показаны результаты расчета точек траектории преследователя в пространстве без учета перехода процесса преследования на плоскость 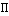 . .
|
|
|
Рис. 8 – Расчет траектории преследователя в пространстве
|
На экран выведены точки 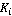 пересечения плоскости пересечения плоскости 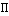 (плоскость (плоскость 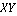 ), плоскости ), плоскости 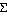 и плоскости и плоскости 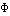 (Рис. 3) и точки пересечения конуса, сферы и плоскости (Рис. 3) и точки пересечения конуса, сферы и плоскости 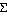 (плоскости параллельного сближения). (плоскости параллельного сближения).
В течении всего итерационного процесса производится анализ взаимного расположения точек положения преследователя 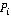 и плоскости и плоскости 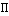 движения цели. Поскольку плоскость движения цели. Поскольку плоскость 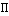 движения цели совпадает с координатной плоскостью движения цели совпадает с координатной плоскостью 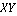 , то достаточно произвести анализ аппликаты преследователя на знак. Как только изменяется знак аппликаты, то происходит возврат на предыдущую рассчитанную точку траектории и производится расчет по другой итерационной схеме. , то достаточно произвести анализ аппликаты преследователя на знак. Как только изменяется знак аппликаты, то происходит возврат на предыдущую рассчитанную точку траектории и производится расчет по другой итерационной схеме.
Показано, что аппликата точки 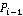 имеет положительное значение, а аппликата точки имеет положительное значение, а аппликата точки 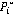 имеет отрицательное значение. Координаты точки имеет отрицательное значение. Координаты точки 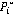 получены в результате пересечения сферы получены в результате пересечения сферы 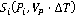 , конуса с осью вращения вдоль вектора , конуса с осью вращения вдоль вектора 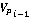 с углом раствора с углом раствора 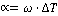 , как на рисунке 3, и плоскости параллельного движения , как на рисунке 3, и плоскости параллельного движения 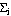 . .
Происходит возврат в точку 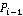 и ищется точка пересечения и ищется точка пересечения 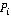 с плоскостью параллельного движения с плоскостью параллельного движения 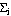 и плоскостью и плоскостью 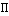 движения цели. движения цели.
В тестовой программе, написанной по материалам статьи, реализован именно такой критерий перехода на плоскость.
|
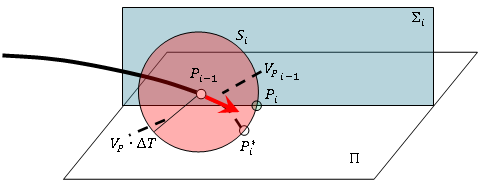
|
|
Рис. 9 – Пересечение сферы, плоскости движения цели и плоскости параллельного сближения
|
IV. Результаты экспериментов
На рисунке 10 показаны результаты работы программы расчета траектории преследователя, преследующего цель, двигающуюся равномерно и прямолинейно. Траектория переходит из движения в пространстве в движение на плоскости.
|

|
|
Рис. 10 – Расчет траектории преследователя
|
Рисунок 10 дополнен ссылкой на анимированное изображение, где возможно посмотреть на процесс преследования.
V. Обсуждение результатов
В предложенной модели расчета траектории преследователя плоскость 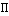 движения цели определена начальной линией визирования движения цели определена начальной линией визирования 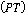 и вектором скорости и вектором скорости 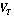 движения цели. Плоскость движения цели. Плоскость 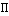 в этом случае служит ограничивающей поверхностью. В тестовой программе реализована такая модель преследования: переход от преследования в пространстве к преследованию на плоскости без захода за плоскость ограничения и с ограничениями по кривизне траектории движения преследователя. в этом случае служит ограничивающей поверхностью. В тестовой программе реализована такая модель преследования: переход от преследования в пространстве к преследованию на плоскости без захода за плоскость ограничения и с ограничениями по кривизне траектории движения преследователя.
В тестовом режиме также при переходе на плоскость было испробовано использование точки 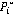 в качестве центра сферы, пересекающей плоскости в качестве центра сферы, пересекающей плоскости 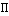 и и 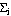 , и построение траектории преследования от нее. , и построение траектории преследования от нее.
VI. Выводы и заключение
В данной статье была предложена кинематическая модель задачи преследования в пространстве. С развитием технологий, систем искусственного интеллекта, технологий спутникового позиционирования движущихся объектов моделирование задач преследования приобрело значимость.
Задач и условий, в которых требуются моделирование итерационных процессов преследования множество. Результаты исследований могут быть востребованы разработчиками беспилотных летательных аппаратов с элементами искусственного интеллекта.
References
1. V. Ya. Volkov, M.A. Chizhik. Graficheskie optimizatsionnye modeli mnogofaktornykh protsessov. / Monografiya, g. Omsk, : Izdatel'sko-poligraficheskii tsentr OGIS, 644099, Omsk, ul. Krasnogvardeiskaya, 9, 101 s., 2009 g.
2. Aizeks R. Differentsial'nye igry. Moskva: Mir, 1967 g..
3. L. S. Pontryagin. Lineinaya differentsial'naya igra ukloneniya/ Tr. MIAN SSSR. 1971. T. 112. S. 30-63.
4. N. N. Krasovskii, A. I. Subbotin. Pozitsionnye differentsial'nye igry/ M, Nauka, 1974 g.
5. Petrosyan L. A. Differentsial'nye igry presledovaniya/ Izd-vo LGU, 222 c., 1977 g.
6. http://dubanov.exponenta.ru Razdel «Odnovremennoe dostizhenie tseli na ploskosti» (data obrashcheniya 22.05.2021)
7. Vagin D. A., Petrov N. N. Zadacha po presledovaniyu skoordinirovannykh begletsov // Izvestiya RAN. Teoriya i sistemy upravleniya. 2001. № 5. Str. 75-79.
8. Bannikov A. S. Nekotorye nestatsionarnye zadachi gruppovogo presledovaniya // Trudy Instituta matematiki i informatiki UdGU. 2013. Vypusk 1 (41), s. 3-46
9. Bannikov A. S. Nestatsionarnaya zadacha gruppovogo presledovaniya // Trudy Matematicheskogo tsentra Lobachevskogo. Kazan': Izd-vo Kazanskogo matematicheskogo obshchestva, 2006, Vyp. 34, str. 26-28.
10. Izmest'ev I.V., Ukhobotov V.I. «Zadacha presledovaniya malomanevrennykh ob''ektov s terminal'nym mnozhestvom v vide kol'tsa», Materialy mezhdunarodnoi konferentsii «Geometricheskie metody v teorii upravleniya i matematicheskoi fizike: differentsial'nye uravneniya, integriruemost', kachestvennye teoriya »Ryazan', 15-18 sentyabrya 2016 g., Itogi nauki i tekhniki. Temat. obz., 148, VINITI RAN, Moskva, 2018, 25-31
11. Video, rezul'taty modelirovaniya zadachi presledovaniya v prostranstve, https://www.youtube.com/watch?app=desktop&v=JlUmh6DTrA4&feature=youtu.be
12. Svidetel'stvo o gosudarstvennoi registratsii programmy dlya EVM № 2020665641. Kinematicheskaya model' metoda parallel'nogo sblizheniya
| 















 This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.
This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.

 Eng
Eng


