
- About

- Journals

- Authors

- Agreements

- Reviewing

- Advertisement

- Services









|
Library
|
Your profile |
 This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.
This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.|
Software systems and computational methods
Reference:
Pritykin, F.N., Nebritov, V.I. (2021). Design of linear surfaces that restrict the range of permissible positions of links of the manipulator mechanisms in implementation of instantaneous states . Software systems and computational methods, 2, 74–90. https://doi.org/10.7256/2454-0714.2021.2.35574
Design of linear surfaces that restrict the range of permissible positions of links of the manipulator mechanisms in implementation of instantaneous states
DOI: 10.7256/2454-0714.2021.2.35574Received: 25-04-2021Published: 04-07-2021Abstract: Linear surfaces are used in various spheres of human activity. One of the most common techniques of designing linear surfaces is based on the three directing curves. In some cases, one of these directing curves is not set, but rather replaced by some geometric condition imposed on the emerging surfaces, which can in form of a certain point correspondence established between the points of the rest two directing curves. The article reviews the example of designing such surfaces, which in an approximate form would restrict the zone that sets the permissible positions of links of the manipulator mechanism of certain given configuration in realization of permissible instantaneous states. The acquired linear surfaces underlie the algorithm for calculation of configurations, which do not intersect the restricted zone in case of a deadlock situation. The result of this research is the computer simulation of the motions of arm and torso mechanism of the Android robot using the obtained algorithm for calculation of configurations. The simulation of motion demonstrates that the use of linear surfaces in analysis of the relative position of the manipulator and restricted zones in the deadlock situations allows reducing the calculation time by 50-60 percent. Such reduction of calculation time is highly demanded in computer control of the arm and torso motions of the Android robot on a real time scale. Keywords: movement synthesis of manipulator, geometric modeling, ruled surface, instant states, android robot, manipulator mechanism, spherical curve, forbidden area, kinematic pair, tapered surfaceThis article written in Russian. You can find original text of the article here . Введение Линейчатые поверхности используются в различных областях деятельности человека. Конструкторы и инженеры используют их при проектировании и изготовлении различных технических устройств, архитекторы при проектировании зданий, сооружений и другое [1-5]. Конструирование линейчатых поверхностей, может осуществляться различными способами [6-11]. Одним из распространенных способов является конструирование линейчатых поверхностей с помощью задания трех направляющих кривых. В некоторых случаях одна из этих направляющих кривых непосредственно не задается, а заменяется каким-либо геометрическим условием, накладываемым на образующие поверхности. Это геометрическое условие может быть задано в виде некоторого точечного соответствия, устанавливаемого между точками двух оставшихся направляющих кривых. Задание линейчатой поверхности двумя направляющими с установлением между их точками взаимно-однозначного соответствия называется инженерным способом задания линейчатых поверхностей [12-13]. Рассмотрим пример конструирования указанных поверхностей, которые в приближенном виде будут ограничивать область Dm, которая задает допустимые положения звеньев механизма манипулятора некоторой заданной конфигурации при реализации допустимых мгновенных состояний. Допустимые мгновенные состояния механизма манипулятора определяют вектором обобщенных скоростей из области допустимых значений (которые соответственно обозначим QN и `Omega` Q) [14-19]. Заметим, что в дальнейшем в представленном исследовании принимается допущение равенства обобщенных скоростей q̇i и приращений обобщенных координат `Delta` qi за одну итерацию. В этом случае компоненты вектора будут следующие QN (q̇1≈`Delta` q1, q̇2≈`Delta` q2, … , q̇n≈`Delta` qn). Где n определяет число обобщенных координат механизма. Верхний индекс обозначений Q определяет принадлежность геометрического объекта многомерному пространству обобщенных скоростей Q. Следовательно, область `Omega` Q принадлежит пространству Q. Постановка задачи Пусть задан пространственный механизм манипулятора массивами длин звеньев, кодов кинематических преобразователей, смещениями вдоль осей координат [16,20,23]. В качестве примера моделирования линейчатых поверхностей рассмотрим механизм андроидного робота [17,23]. Кинематическая схема указанного механизма изображена на рисунке 1а. Число обобщенных координат этого механизма n = 5. Синтез движений данного механизма осуществляется с обеспечением движения центра выходного звена (ВЗ) по заданной траектории при произвольной его ориентации. В этом случае размерность вектора скоростей ВЗ будет равна трем r = 3, V(Vх, Vy, Vz). При синтезе движений исследуемого механизма существует двигательная избыточность равная р = n – r = 2 [16,24]. При реализации значений вектора QN из области `Omega` Q звенья механизма андроидного робота в неподвижной системе координат располагаются в определенной окрестности около исходной конфигурации. Эта допустимая области возможных положений звеньев в работах [16,24] обозначена Dm. Размеры указанной области Dm зависят от заданной точности позиционирования центра ВЗ `delta` на траектории его движения. Для конструирования линейчатых поверхностей в приближенном виде, ограничивающих указанные допустимые области Dm , исследуем положения узловых точек О1÷О12 механизма манипулятора в исходном положении (см. рис. 1а) и при реализации значений вектора QN[24]. Под реализацией мгновенного состояния или значения вектора QN будем понимать новое положение механизма манипулятора, определяемого обобщенными координатами: q1 = q1 + `Delta` q1, q2 = q2 + `Delta` q2, … , qn = qn + `Delta` qn. (1) На рисунке 1аб представлены точки О1, О2, …, Оj, которые задают положения узловых точек совпадающих с центрами систем координат, связанных со звеньями механизма манипулятора. Для рассматриваемого примера количество узловых точек j = 12 [16]. Некоторые узловые точки могут совпадать между собой. Данное количество узловых точек равно числу систем координат, используемых при задании модели кинематической цепи механизма манипулятора. На рисунке 1б изображена сфера `Sigma` единичного радиуса и положение сферической кривой lсф на этой сфере, определяющей телесный угол сервиса [21,25,26]. Телесный угол сервиса при этом определяют образующие линейчатой поверхности `Psi` 1. Каждая образующая линейчатой поверхности `Psi` 1 определяется точками О12 и О'11. Множество положений точки О'11 при реализации мгновенных состояний находятся на поверхности сферы `Sigma` сф с центром в точке О12 и радиусом равным отрезку О12О'11. Указанная сфера на рисунке 1б не показана. Точка О'11 полученная реализацией (1) в общем случае может занимать произвольные положения на сфере `Sigma` сф. Положение точки О'11 на сфере `Sigma` сф определяется углами `alpha` и `beta` (см. рис. 1аб). Способ определения данных углов и образующих конической поверхности `Psi` 1 задающих телесный угол сервиса изложен в работах [25, 26]. Положение точки О'11 может быть задано углами `alpha` р = `alpha` и `beta` р = `beta` на условной развертке сферы `Sigma` (см. рис. 1в). Поверхность сферы `Sigma` единичного радиуса (см. рис. 1в) на условной развертке разделена на 12 равных секторов. а
б в Рис. 1 Моделирование линейчатой конической поверхности `Psi` 1, образованной положениями отрезка О'11О12 звена механизма руки и туловища андроидного робота реализацией мгновенных состояний: а – кинематическая схема механизма; б – положения образующих конической поверхности `Psi` 1 задающей телесный угол сервиса; в – условная развертка сферы `Sigma` единичного радиуса Метод построения направляющих кривых и образующих линейчатых поверхностей Зададим положение плоскостей `alpha` 3, `alpha` 6, `alpha` 7, …, `alpha` j (см. рис. 2), где j – номер плоскости αj, проходящей через j-ю узловую точку Оj. Плоскости `alpha` 3, `alpha` 6, `alpha` 7, …, `alpha` 11 проходят через точки О3, О6, …, О11 и перпендикулярны осям звеньев О3О4, О5О6, О7О8 и т. п. (О3`in` α3, α3`_|_` О3О4, О6`in` α6, α6`_|_`О5О6, О7`in` α7, α7`_|_`О7О8, О10`in`α10, α10`_|_` О9О10, О11`in` α11, α11`_|_`O11О12, О12`in` α12, α12`_|_` О11О12). Знак `in` определяет принадлежность точки геометрическому объекту `alpha` j. Заметим, что узловые точки О8 и О9 находятся в центре вращательной кинематической пары, ось которой совпадает с осями звеньев. Поэтому звенья задаваемые узловыми точками О8О7 и О10О9 определяются положением отрезка прямой О7О10. Рис. 2 Определение положения и формы направляющих линий `mu` `alpha` 3, `mu` `alpha` 6, `mu` `alpha` 7, и `mu``alpha` 10 линейчатых поверхностей `Psi`2 и `Psi`3
Следовательно, через заданные точки нет необходимости строить плоскости `alpha`8 и `alpha`9 (О8`in``alpha`8, `alpha`8`_|_`О8О7 и О9`in`` ``alpha`9, `alpha`9`_|_`О9О10). Аналогичным образом также нет необходимости построения плоскостей `alpha`4 и `alpha`5 (О4`in``alpha`4, `alpha`4`_|_`О4О3 и О5`in``alpha`5, `alpha`5`_|_`О5О6). На рисунке 2 плоскости `alpha`6, `alpha`11 не изображены с целью уменьшения геометрической информации, представленной на этом рисунке. Пусть при реализации значений вектора QN из области допустимых значений `Omega`Q точки О3÷О12 из начального положения смещаются в положения О'3÷О'12. Заметим, что точки О12 и О'12 имеют между собой расстояние d меньшее заданной допустимой точности позиционирования `delta` [20,24]. В тестовых расчетах значение данного параметра принято `delta` = 2 мм. Спроецируем с помощью ортогонального проецирования точки О'3÷О'12 соответственно на плоскости `alpha`3, `alpha`6, `alpha`7, …, `alpha`j по направлениям проецирования, определяемым отрезками О3О4, О5О6, О7О8 и т. п. Указанные проекции точек О'3÷О'12 на плоскостях `alpha`3, `alpha`6, `alpha`7, …, `alpha`j определяют соответственно точки О`alpha`3, О`alpha`6, О`alpha`7, …, О`alpha`11 (см. рис. 2). Разделим плоскости `alpha`6, …, `alpha`11 на несколько равных секторов (в рассматриваемом примере указанные плоскости разделены на двенадцать равных секторов, определяемых углом 30°). Для нахождения положения первого сектора (I) в указанных плоскостях зададим оси х`alpha`6, х`alpha`7, х`alpha`10 и х`alpha`12. Данные оси задают начала отсчета первого сектора. Ось х`alpha`12 совпадает с осью хn системы координат Оnхnynzn связанной с ВЗ (см. рис. 2). Зададим точку А`alpha`12 `in` х`alpha`12. Для определения положения оси х`alpha`11 необходимо найти проекцию точки А`alpha`12 на плоскости `alpha`11 по направлению проецирования, заданного отрезком О11О12. Эту точку определяет проекция А`alpha`11. Далее точку А`alpha`11 необходимо спроецировать на плоскость α10 по направлению проецирования заданного отрезком О9О10. Полученную проекцию обозначим А`alpha`10. Ось х`alpha`10 проходит через точки О10 и А`alpha`10 (см. рис. 2). Положение осей х`alpha`6 и х`alpha`7 определяется аналогичным образом. При этом вначале точка А`alpha`10 проецируется по направлению, заданному отрезком О9О10 на плоскость `alpha`7, а затем точка А`alpha`7 проецируется по направлению, заданному отрезком О6О5 на плоскость `alpha`6. Пусть первый сектор плоскостей `alpha`7 и `alpha`10 определяется углом 30° отложенном от осей х`alpha`7, и х`alpha`10 по часовой стрелки при направлении взгляда от точки О11 к О12, от точки О9 к О10 и т. п. Полученные сектора на рисунке показаны в заштрихованном виде. При реализации значений вектора обобщенных скоростей QN из области `Omega`Q определим в каждом секторе такие точки Оmax`alpha`3, Оmax`alpha`6, …, Оmax`alpha`11 которые будут иметь максимальное удаление соответственно от точек О3, О6, …, О11. Заметим, что каждая точка Оmax`alpha`j заносится в базу данных определенного сектора плоскостей `alpha`7 и `alpha`10 если выполняются условия: d`mu alpha`10(k+1) > d`mu alpha`10(ki)max, d`mu alpha`7(k+1) > d`mu alpha`10(k+1) / 2, (2) где d`mu alpha`10(k+1) - расстояние от точки О`alpha`10 до узловой точки О10 в плоскости `alpha`10 соответствующего сектора для следующей расчетной конфигурации k+1, d`mu alpha`10(ki)max – максимальное расстояние полученное на предыдущих итерациях связанных с расчетом положения конфигурации с номером ki, d`mu alpha`7(k+1) - соответственно расстояние между точками О`alpha`7 и О7 в плоскости `alpha`7 соответствующего сектора. Совокупность данных точек в различных секторах определяет кривые `mu``alpha`6, `mu``alpha`7 и `mu``alpha`10 принадлежащие соответственно плоскостям `alpha`6, `alpha`7, и `alpha`10 (см. рис. 2). В качестве направляющей линии в плоскости `alpha`3 выступает отрезок прямой `mu``alpha`3. Кривые `mu``alpha`6, `mu``alpha`7 и `mu``alpha`10 могут быть построены более точно, если увеличить количество исследуемых секторов. Сконструируем линейчатые поверхности `Psi`2 и `Psi`3, в качестве направляющих кривых, которых будут выступать отрезок `mu``alpha`3 и кривая `mu``alpha`6, а также кривые `mu``alpha`7 и `mu``alpha`10. По аналогии с инженерным способом задания линейчатых поверхностей соответствия между точками линий `mu``alpha`3 и `mu``alpha`6, а также кривых `mu``alpha`7 и `mu``alpha`10 будет задавать принадлежность точек Оmax`alpha`3, Оmax`alpha`6, Оmax`alpha`7, и Оmax`alpha`10 кривых соответствующим секторам плоскостей `alpha`6, `alpha`7 и `alpha`10. Для установления соответствия точек направляющих линий линейчатой поверхности `Psi`3 на отрезке `mu``alpha`3 задаются точки 1`alpha`3, 2`alpha`3, … , (см. рис. 2в). У линейчатой конической поверхности `Psi`1, определяющей положениями звена ограниченного точками О11О12 (это звено называют осью схватоносителя) вершиной будет являться точка О12, а направляющей кривой `mu``alpha`11`sub``alpha`11. Указанная кривая `mu``alpha`11 и плоскость `alpha`11 на данном рисунке не показаны. При этом принято допущение о том, что точки О12 и О'12 совпадают. Хотя на самом деле данные точки не могут совпадать, но расстояние между ними не превышает заданную минимальную величину равную заданной точности позиционирования `delta`[25]. Линейчатую поверхность `Psi`2 ограничивающую допустимые положения звеньев О7О8 и О9О10 задают соответственно направляющие кривые `mu``alpha`7`sub``alpha`7 и `mu``alpha`10`sub``alpha`10. Образующую l`Psi`2 линейчатой поверхности `Psi`2 зададим уравнениями двух проекций этой прямой: `{(y = ax + b),(z = cx+ d):}` (3) Пусть направляющую кривую `mu``alpha`7 определяют зависимости: x = f1(`beta`), y = f2(`beta`), (4) z = f3(`beta`), где `beta` определяет угол, который задает положения точек Оmax`alpha`3, Оmax`alpha`6, …, Оmax`alpha`11 в плоскостях `alpha`6, `alpha`7 и `alpha`10 в полярных координатах в каждом секторе (см. рис. 2). Угол `beta` задается в базе данных B`alpha`j точек направляющих кривых `mu``alpha`j. Координаты точек Оmax`alpha`6, Оmax`alpha`7, и Оmax`alpha`10 в неподвижной системе координат могут быть рассчитаны с использованием матриц М0,k задающих переход от системы координат связанной с k-ым звеном к неподвижной системе координат. Условие пересечения образующей l`Psi`2 линейчатой поверхности `Psi`2 с направляющей кривой `mu``alpha`7 записывается следующим образом: f2(`beta`) = а(f1(`beta`)) + b, f3(`beta`) = с(f1(`beta`)) + d.(5) При задании значения параметра `beta` получаем функцию f(а,b,с,d) = 0. Вторая направляющая кривая `mu``alpha`10 задается функциями : х = f4(`beta`), y = f5(`beta`),(6) z = f6(`beta`). Условие пересечения образующей со второй направляющей кривой `mu``alpha`10 будет следующим:
f5(`beta`) = а(f4(`beta`)) + b, f6(`beta`) = с(f4(`beta`)) + d.(7) Тогда при задании значения `beta` определяются положения соответствующих точек Оmax`alpha`6, и Оmax`alpha`11 (4) (6) в каком либо секторе на кривых `mu``alpha`7 и `mu``alpha`10 и уравнения (4) и (6). Уравнения (5) и (7) задают значения коэффициентов а, b, с и d проекций образующей линейчатой поверхности, так как получаем линейную систему уравнений с четырьмя неизвестными а, b, с и d. Следовательно, для каждого значения параметра `beta` определяется положение прямолинейной образующей l`Psi`2 поверхности `Psi`2. На рисунке 3а представлены изображения кривых, располагающихся в соответствующих плоскостях `mu``alpha`7`sub``alpha`7 и `mu``alpha`10`sub``alpha`10 для конфигурации заданной вектором Lt (25°, 20°, -35°, -25°, -65°). а б Рис. 3 Положения направляющих линий `mu``alpha`7 и `mu``alpha`10 поверхности `Psi`2 для конфигурации заданной вектором Lt (25°, 20°, -35°, -25°, -65°): а – кривая `mu``alpha`7 `sub``alpha`7; б – кривая `mu``alpha`10`sub``alpha`10
На кривых `mu``alpha`7 и `mu``alpha`10 обозначены точки 1`alpha`7, 2`alpha`7, …, 12`alpha`7, 1`alpha`10, 2`alpha`10, …, 12`alpha`10, которые соответствуют положению точек Оmax`alpha`3, Оmax`alpha`6, …, Оmax`alpha`11 в каждом из двенадцати секторов. Между точками двух кривых `mu``alpha`7 и `mu``alpha`10 существует однозначное соответствие. Точке 1`alpha`7 на кривой `mu``alpha`7 соответствует точка 1`alpha`10 на кривой `mu``alpha`10. По аналогии с инженерным способом задания линейчатых поверхностей, направляющие кривые `mu``alpha`7 и `mu``alpha`10 и соответствие точек этих кривых определяют линейчатую поверхность `Psi`2 (см. рис. 4а). Эта поверхность приближенно ограничивает область допустимых положений звена определяемого опорными точками О7 и О10 при реализации допустимых значений вектора QN из области `Omega`Q. Аналогичным образом находится линейчатая поверхность `Psi`3, ограничивающая допустимые положения звеньев заданных узловыми точками О3 и О6. При этом в качестве направляющей линии в плоскости `alpha`3 выступает отрезок прямой, на котором заданы точки 1`alpha`3, 2`alpha`3, …, 12`alpha`3 (см. рис. 4б). На рисунке 4в представлена линейчатая поверхность `Psi`1.
а 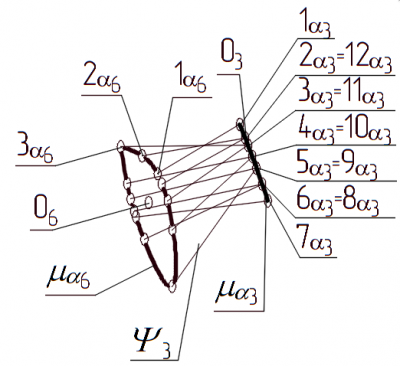 б
в 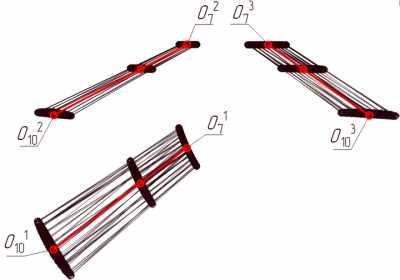 г
Рис. 4 Положения образующих линейчатых поверхностей `Psi`1, `Psi`2, и `Psi`3 для конфигурации заданной вектором Lt (25°, 20°, -35°, -25°, -65°): а - положение образующих l`Psi`2 линейчатой поверхности `Psi`2 ; б – положение образующих l`Psi`3 линейчатой поверхности `Psi`3 ; в - положение образующих l`Psi`1 линейчатой поверхности `Psi`1; г – положения звена О7О10 при реализации мгновенных состояний
Множество положений звена О7О10 при реализациях мгновенных состояний на трех плоскостях проекций представлено на рисунке 4г. Пусть при синтезе движений механизма манипулятора возникает тупиковая ситуация. Заметим, что при синтезе движений при возникновении пересечения, каково либо из звеньев с запретной зоной с целью сокращения времени расчетов исследуется ограниченное число конфигураций задающих вектором приращений QN и значениями `Delta`ki (в тестовых примерах данное максимальное количество конфигураций равно двадцати)[24]. Параметры ki определяют положение точки NQ заданной вектором QN в р-плоскости ГQ, которая задана линейной системой уравнений [16,22-24]: V = JAQN, (8) где J – определяет матрицу частных передаточных отношений, А – матрицу диагонального вида, задающую значения весовых коэффициентов обобщенных скоростей. Учитывая то, что общее количество допустимых конфигураций заданных областью `Omega`` `Q может достигать несколько сотен, целесообразно исследовать ограниченное их число при возникновении пересечения механизма с запретной зоной. Это объясняется необходимостью сокращения времени расчетов. Например, когда все допустимые значения вектора QN из двадцати исследованы, которые задают конфигурации, пересекающие запретные зоны, то данное положение механизма принимается за тупиковую ситуацию. Для этого случая необходимо вычислить положения линейчатых поверхностей `Psi`1, `Psi`2 и `Psi`3. При этом для каждой из точек 1`alpha`7, 2`alpha`7, …, 12`alpha`7, 1`alpha`10, 2`alpha`10, …, 12`alpha`10 кривых `mu``alpha`7 и `mu``alpha`10 в базе данных сохраняются значения обобщенных координат qi и угол `beta`, который задает положение точек в полярных координатах в плоскостях `alpha`j. Для сокращения времени расчета положения линейчатых поверхностей `Psi`1, `Psi`2 и `Psi`3 условие пересечения конфигураций с запретными зонами не определяется. Алгоритм моделирования движений с выходом механизма манипулятора из тупиковой ситуации После вычисления направляющих кривых `mu``alpha`3, `mu``alpha`6, `mu``alpha`7, `mu``alpha`10 и `mu``alpha`11, а также линейчатых поверхностей `Psi`1, `Psi`2 и `Psi`3, определяются пересечения образующих этих поверхностей с запретными зонами. Пусть образующая l`Psi`2 поверхности `Psi`2 соответствующая сектору 11 пересекает запретную зону. Данная образующая проходит через точки 11`alpha`7 и 11`alpha`10. Для этого случая противоположным сектором по отношению к сектору 11 будет сектор с номером 5. Тогда из базы данных точек направляющих кривых `mu``alpha`7 и `mu``alpha`10 необходимо исследовать конфигурации заданные точками 5`alpha`7 и 5`alpha`10. Данные точки 5`alpha`7 и 5`alpha`10 находятся на противоположных сторонах секторов 11 плоскостей `alpha`7 и `alpha`10. Следует отметить, что реальные положения отрезка, заданного узловыми точками О7О10 звеньев О7О8 и О9О10 при реализации мгновенных состояний, не будут совпадать с положением образующих линейчатой поверхности `Psi`2 (например, проходящих через точки 5`alpha`7 и 5`alpha`10 или точки 11`alpha`7 и 11`alpha`10). Однако каждая из указанных двух точек 5`alpha`7 и 5`alpha`10 будет задавать в базе данных два значения вектора Lt(q1, q2, …, qn) обобщенных координат, которые будут задавать две конфигурации проекции узловых точек которой О7 и О10 будут принадлежать сектору 5 противоположному сектору 11. А следовательно указанные конфигурации находятся на большем удалении от запретной зоны чем конфигурации проекции узловых точек О7 и О10 которых будут принадлежать сектору 11. Это объясняется тем, что образующая линейчатой поверхности `Psi`2 сектора 11 пересекает запретную зону. Использование указанных двух конфигураций проходящих через точки 5`alpha`7 и 5`alpha`11 позволяет исключить итерационный поиск значения вектора QN с определением пересечения каждой полученной конфигурации (количество которых может достигать нескольких сотен) с запретными зонами. Это позволяет сократить время вычислений на 50 – 60 процентов. На рисунке 5 представлена схема алгоритма вычисления конфигураций, не пересекающих запретные зоны при возникновении тупиковых ситуаций и использовании образующих линейчатых поверхностей `Psi`1, `Psi`2 и `Psi`3. Рис. 5 Алгоритм вычисления конфигураций, не пересекающих запретные зоны с использованием анализа положения образующих линейчатых поверхностей `Psi`i Результаты моделирования движений механизма манипулятора с выходом из тупиковой ситуации На рисунке 5 приняты следующие обозначения: 1 – ввод исходных данных qi - исходные значения обобщенных координат, li -длины звеньев механизмов, nkod - коды преобразований систем координат [16]), lsmi - смещения вдоль осей координат связанных со звеньями механизма, Ац – координаты целевой точки центра ВЗ механизма, n – максимальное число обобщенных координат, Ктmax = 20 – максимальное число конфигураций определяющих тупиковую ситуацию, Кт = 0, k = 0, ddmin - минимально заданное расстояние центра ВЗ от целевой точки Ац, `Delta`kiT - интервал изменения значения параметра ki при построении движения по заданной траектории цента ВЗ [23], `Delta`kiЛ - интервал изменения значения параметра ki при вычислении положения направляющих кривых `mu``alpha`j линейчатых поверхностей `Psi`j. Данный интервал на порядок меньше значения `Delta`kiT; 2 – вычисление V(Vх, Vy, Vz) - вектора определяющего скорости простейших движений центра ВЗ, расчет J - матрицы частных передаточных отношений (7)[16,23], вычисление QM - вектора обобщенных скоростей соответствующего критерию минимизации объема движения [16,23]; 3 – вычисление следующей конфигурации Lt+1 (q1 + `Delta`q1, q2 + `Delta`q2, … , qn + `Delta`qn) (1) , где `Delta`qi компоненты вектора QM или QN; 4 – определение условия пересечения конфигурации Lt+1 с запретной зоной Р; 5 - сохранение в базе данных конфигурации Lt+1 как разрешенной и переход к расчету следующей конфигурации на заданной траектории центра ВЗ; 6 – цель достигнута dd < ddmin (где dd – текущее расстояние центра ВЗ от заданной целевой точки Ац); 7 - Кт < Ктmax; 8 - вычисление вектора QN (при значении приращения `Delta`kiT), Кт = Кт + 1; 9 – вычисление положения плоскостей `alpha`j и точек кривых `mu``alpha`j (при значении приращения `Delta`kiЛ), задание в базе данных точек В`alpha`j`->`1`alpha`j - qi`alpha`j (q1`alpha`jq2`alpha`j, … , qn`alpha`), `beta`1`alpha`j, 2a`alpha`j- qi`alpha` (q1`alpha`jq2`alpha`j, … , qn`alpha`j) `beta`2`alpha`j, где В`alpha`j база данных точек 1`alpha`j, 2`alpha`j кривых `mu``alpha`j, принадлежащих плоскостям `alpha`j; 10 – вычисление положения образующих l`Psi`i поверхностей `Psi`i (4)(6); 11 – определение образующих l`Psi`, пересекающих запретную зону Р, и точек Bl базы данных В`alpha`j,через которые проходят данные образующие. Определение номеров секторов, которым принадлежат точки Bl, задающие образующие пересекающие препятствия Рз; 12 – определение образующих линейчатых поверхностей l'`Psi` и точек направляющих кривых `mu``alpha`j, располагающихся на противоположных секторах плоскостей `alpha`j, выбор конфигураций из базы данных В`alpha`j соответствующих точкам, через которые проходят образующие l'`Psi`. На рисунке 6 представлены результаты расчета промежуточных конфигураций при использовании линейчатых поверхностей `Psi`1, `Psi`2, `Psi`3 и алгоритма, представленного на рисунке 5, с целью преодоления тупиковых ситуаций.
Рис. 6 Результаты компьютерного моделирования движений механизма андроидного робота с использованием линейчатых поверхностей при анализе взаимного положения манипулятора и запретных зон
На рисунке 6 проекции точек Оц1, Оц2, Оц3 и Он1, Он2, Он3 определяют соответственно положение начальной и целевой точек. Проекции Р1, Р2 и Р3 задают положение запретной зоны. Выводы и заключение Результаты компьютерного моделирования движений механизма руки и туловища андроидного робота показывают, что использование линейчатых поверхностей при анализе взаимного положения манипулятора и запретных зон в тупиковых ситуациях позволяет сократить время вычислений на 50-60 процентов. Полученное сокращение времени расчета является наиболее востребованным при компьютерном управлении движением руки и туловища андроидного робота в реальном масштабе времени. References
1. Gershman, I.P. Konstruirovanie poverkhnostei putem vydeleniya ikh nepreryvnykh lineichatykh karkasov iz mnogoparametricheskikh mnozhestv linii // Trudy UDN im. P. Lumumby. T. 26: Matematika.: Prikladnaya geometriya. Moskva, 1967. – Vyp. 3. – S. 33 – 47.
2. Zeiliger, D. N. Kompleksnaya lineichataya geometriya. – Moskva:. 1934. – 195 s. 3. Ivanov, G. S. Teoreticheskie osnovy nachertatel'noi geometrii: Uchebnoe posobie. – Moskva: Mashinostroenie, 1998. – 158 s. 4. Il'yasova, O.B. Formalizovannyi apparat konstruirovaniya lineichatykh poverkhnostei / O.B. Il'yasova, V.I. Glukhov/ Omskii nauchnyi vestnik – 2008, №1 (64) s. 20 – 23. 5. Kokareva, Ya.A. Sintez uravnenii lineichatykh poverkhnostei s dvumya krivolineinymi i odnoi pryamolineinoi napravlyayushchimi / Ya. A. Kokareva. // Geometriya i grafika. – 2018. – T. 6. – № 3. – S. 3 – 12. 6. Korotkii, V.A. Komp'yuternoe modelirovanie tekhnicheskikh poverkhnostei / V.A. Korotkii , E.A. Usmanova, L.I. Khmarova. // Geometriya i grafika. – 2015. – T. 3 – № 4. – S. 19 – 26. 7. Mikhailenko, V.E. Formoobrazovanie obolochek v arkhitekture / V.E. Mikhailenko, V.S. Obukhova, A.L. Podgornyi. – Kiev: Budivel'nik, 1972. – 207s. – Tekst : neposredstvennyi. 8. Panchuk, K.L. Differentsial'no-geometricheskii metod obrazovaniya lineichatykh razvertyvayushchikhsya poverkhnostei / K.L. Panchuk, A.S. Niteiskii. –// Vestnik KuzGTU. – 2014. – № 1 (101). – S. 70 – 73. 9. Rachkovskaya, G.S. Geometricheskoe modelirovanie i grafika kinematicheskikh lineichatykh poverkhnostei na osnove triady kontaktiruyushchikh aksoidov // Geometriya i grafika. – 2016. – T. 4. – № 3. – S. 46 – 52. 10. Sal'kov, N.A. Obshchie printsipy zadaniya lineichatykh poverkhnostei. Chast' 2 / N.A. Sal'kov. // Geometriya i grafika. — 2019. — T. 7. — № 1. — S. 14 – 27. 11. Panchuk, K. L. Geometricheskoe modelirovanie v inzhenernoi i komp'yuternoi grafike : ucheb. posobie / K. L. Panchuk, A. A. Lyashkov, N. V. Kaigorodtseva, L. M. Leonova. – Omsk : Izd-vo OmGTU, 2015. – 148 s. 12. Tevlin, A.M. Konstruirovanie nepreryvnykh karkasov obvodov lineichatykh poverkhnostei metodom kinematicheskikh diagramm / A.M. Tevlin, E.E Manasherov. // Kinematicheskie metody konstruirovaniya tekhnicheskikh poverkhnostei. – M., 1979. – Vyp. 213. – S. 59 – 68. 13. Tevlin, A.M Kurs nachertatel'noi geometrii (na baze EVM): Uchebnoe posobie dlya inzh.-tekhn. vuzov /A.M. Tevlin, G.S. Ivanov, L.G.Nartova, V.I. Yakunin/ Moskva : Vyssh. Shkola, 1983.-175 s. 14. Pritykin, F. N. Graficheskoe predstavlenie telesnogo ugla i okruzhayushchego prostranstva ruki pri realizatsii mgnovennykh sostoyanii // Problemy mashinovedeniya i nadezhnosti mashin, 2002. – №3 – s. 93-101. 15. Pritykin, F. N. Obobshchennyi metod opredeleniya ugla servisa dlya ploskikh nezamknutykh mekhanizmov manipulyatorov na osnove analiza mgnovennykh sostoyanii manipulyatorov / F. N. Pritykin, O. I. Gordeev // Mekhatronika, avtomatizatsiya, upravlenie, 2014. – №4 – S. 41-45. 16. Pritykin, F. N. Virtual'noe modelirovanie dvizhenii robotov, imeyushchikh razlichnuyu strukturu kinematicheskikh tsepei: monografiya / F. N. Pritykin. – Omsk: Izd-vo OmGTU, 2014. – 172 s. 17. Pritykin, F. N. Opredelenie formy i razmerov oblasti v shestimernom prostranstve zadayushchei dopustimye mgnovennye sostoyaniya mekhanizma ruki antropomorfnogo robota / F. N. Pritykin, V. I. Nebritov // Programmnye sistemy i vychislitel'nye metody. — 2019.-№ 4.-S.115-124. 18. Pritykin, F. N. Sposob preodoleniya tupikovykh situatsii pri dvizhenii do tselevoi tochki po proizvol'noi traektorii tsentra vykhodnogo zvena/ F. N. Pritykin, V. I. Nebritov // Vestnik komp'yuternykh i informatsionnykh tekhnologii – 2019.-№ 12.-S. 3-9. 19. Nebritov, V. I. Issledovaniya mgnovennykh sostoyanii ploskikh mekhanizmov manipulyatorov pri zadannom dvizhenii vykhodnogo zvena/ V. I. Nebritov, F. N. Pritykin // Teoriya mashin i mekhanizmov – 2020 – t. 18 – № 2 (64)-S.81-90. 20. Pritykin, F. N. Analiz pokazatelei manevrennosti mekhanizmov manipulyatorov, imeyushchikh razlichnuyu strukturu kinematicheskikh tsepei / F. N. Pritykin, E. E. Chukavov // Mekhatronika, avtomatizatsiya, upravlenie, 2013. – №1 – s. 35-39. 21. Lebedev, P. A. Analiticheskii metod opredeleniya koeffitsienta servisa manipulyatora // Problemy mashinostroeniya i nadezhnosti mashin, 1991. – №5. – s. 93 – 98. 22. Whitney D. E. The Mathematics of Coordinated Control of Prosthetic Arms and Manipulators / D. E. Wihtney // J. Dyn. Sys., Meas., Control, 2010. – №94(4). – pp. 303-309 23. Kobrinskii, A. A. Manipulyatsionnye sistemy robotov / A. A. Kobrinskii, A. E. Kobrinskii. – M.: Nauka. 1985. – 343 s. 24. Pritykin, F.N. Vizualizatsiya lineinykh smeshchenii uzlovykh tochek pri realizatsii mgnovennykh sostoyanii razlichnykh konfiguratsii ruki androidnogo robota /F. N. Pritykin, Khomchenko V.G., Yanishevskaya A.G., V. I. Nebritov // Geometriya i grafika – 2019. Tom 7 – vyp. 3.-S. 51-59. 25. Pritykin, F.N. Opredelenie ugla servisa ruki androidnogo robota metodom sinteza malykh dvizhenii osi skhvatonositelya po vektoru skorostei /F. N. Pritykin, V. I. Nebritov // Dinamika sistem, mekhanizmov i mashin. – 2018. – t. 6. №2., – S. 276–281. 26. Pritykin F. N. and Nebritov V.I. Definition of service angle of android’s robot hand by method of small movements of gripper’s axis synthesis by speed vector – AMSP/IOP Conf. Series: Journal of Physics: Conf. Series – 2019 – Vol. 1210. – pp. 012115-1 – 012115-6. DOI:10.1088/1742-6596/1210/1 /01211 |


 Eng
Eng


