The selection of continuous wavelet transform basis for finding extrema of biomedical signals

ВВЕДЕНИЕ

В последнее время широкое распространение для анализа нестационарных сигналов получили частотно-временные методы, например, вейвлет-анализ, дающие заметные преимущества по сравнению с классическим спектральным анализом и позволяющие получить временные локализации спектральных компонент сигнала. Все преимущество вейвлет-анализа заключается в возможности выбора базиса среди большого количества вейвлетов.

Выбор анализирующего вейвлета, как правило, определяется тем, какую информацию необходимо извлечь из исследуемого сигнала. Каждый вейвлет имеет характерные особенности, как во временном, так и в частотном пространстве. Поэтому с помощью разных вейвлетов можно полнее выявить и подчеркнуть те или иные свойства анализируемого сигнала. Выбор анализирующей вейвлет-функции для создания базиса вейвлет-преобразования является одним из вопросов, успешность решения которой влияет на успешность использования вейвлет-анализа в решаемой задаче. Обход этого вопроса отталкивает начинающих в этой области исследователей от использования вейвлет-анализа или значительно ссужает область его применения. Неудачный выбор конкретной формы вейвлета может привести к невозможности решения задачи ^[1]. Универсальное ранжирование базисов и свойств вейвлет-преобразования по предпочтительности предположительно невозможно ^[2]. При этом в большинстве связанных с вейвлет-анализом публикаций базис либо априорно задан или критерии и обоснования выбора базиса остаются неописанными.

Выбор вейвлет-функции особенно важен при непрерывном вейвлет-преобразовании, где результат преобразования трехмерный непрерывный вейвлет-спектр. Это затрудняет его анализ, который зачастую ограничивается визуальным анализом проекции вейвлет-спектра на оси масштаб-время. Это также усложняет выбор вейвлет-функции, так как при смене вейвлета в проекции вейвлет-спектра иногда происходят многочисленные изменения неподдающиеся анализу. Основным свойством непрерывного вейвлет-преобразования является локальность и избыточность представления сигнала ^[5], что позволит более детально анализировать локальные особенности сигналов, что перспективно в задаче нахождения экстремумов в сигнале и экстремумов их производной при наличии шума. Особенно важна эта задача в анализе биомедицинских сигналов ^[6-8], где требуется идентификация физиологических событий на основе нахождения экстремумов сигнала. Так для корректного анализа временных параметров сигнала требуется выбрать вейвлет–функцию, акцентируя внимание на корректности передачи временной структуры сигнала и простоту ее интерпретации. Поэтому целесообразно найти вейвлет–функцию, которая максимально адекватно передает положения точек экстремумов сигнала и ее производной. Применение непрерывного вейвлет-спектра для поиска точек экстремума является нетипичной задачей, хотя является задачей локального частотно-временного анализа сигнала как и большинство решаемых вейвлет-анализом задач. Данное обоснование выбора анализирующего вейвлета может быть полезно для подобных задач в смежных областях применения ^[9].

Цель данной работы показать методику обоснования выбора анализирующей вейвлет-функции для использования ее в задаче локализации точек экстремумов цифрового сигнала.

ПРИМЕРЫ НЕУДАЧНОГО ВЫБОРА ВЕЙВЛЕТА

Для выбора вейвлетов были сравнены в действии разные вейвлеты на модельных сигналах. Уменьшая количество подходящих нам анализирующих вейвлетов, в результате анализа получим анализирующую вейвлет-функцию, которая наилучшим образом передает локальную структуру сигнала. Для этого исследовались вейвлет-спектры модельных сигналов и определялись погрешности нахождения расположения точек экстремумов и диапазон масштабов, где данные точки находятся с малой погрешностью.

Первый сигнал,представленный на рис. 1, представляет собой простую синусоиду

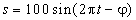
По оси абсцисс – время в секундах, по оси ординат – амплитуда в милливольтах. Примеры выбора вейвлета неудачного для анализа локальных особенностей в сигнале представлены на рис. 1 ниже исходного сигнала. В заголовке графиков название вейвлета, по оси абсцисс – время в секундах, по оси ординат – масштаб в секундах. Обозначение 'sym', взятое из ^[3], значит симлеты, ортогональные вейвлеты с компактным носителем не имеющие аналитического вида, цифрой обозначается порядок этого вейвлета.

Видно, что для sym2, sym3,sym6, sym7 можно подобрать масштаб, на котором находятся экстремумы синусоиды, но так как структура вейвлет – спектра имеет наклон, то по мере изменении масштаба ошибка нахождения экстремумов будет увеличиваться. При использовании sym8, sym9 и sym16 вейвлет – спектры имеют нечеткие структуры ниже масштаба 0.1 сек., что затруднит нахождение экстремумов. Данный вывод был сделан при разборе вейвлет-коэффициентов на конкретных масштабах, в дальнейшем мы разберем этот разбор на примере более подходящего выбора.

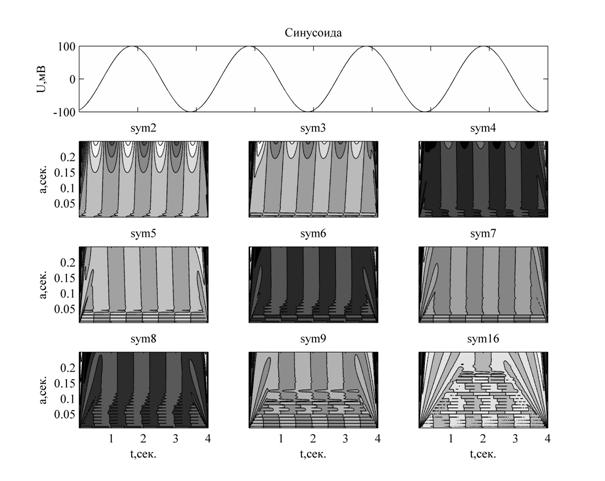
Рис. 1. Примеры неудачного выбора вейвлета для определения экстремумов синусоиды

ПРИМЕРЫ ВЫБОРА ВЕЙВЛЕТА, ПОДХОДЯЩЕГО ДЛЯ ПОИСКА ЭКСТРЕМУМОВ

Проанализировав наборы вейвлет – спектров синусоиды, построенных на основе разных вейвлет – функций, были выбраны следующие вейвлет – функции для дальнейшего рассмотрения их в качестве основного для анализа особенностей сигнала:

· 'Haar' – вейвлет Хаара

· 'bior1.3','bior1.5'– биортогональные сплайн вейвлеты, представляющий собой пару вейвлетов, по одной из которых ведется анализ сигнала, по другой – восстановление, цифрами обозначают порядки вейвлетов, задаются фильтрами;

· 'rbio3.1' – обратные биортогональные сплайн вейвлеты;

· 'gaus1', 'gaus2', 'gaus3', 'gaus4'- вейвлеты, основанные на дифференциале функции Гаусса, цифрой и m обозначен порядок

· 'cgau1'; 'cgau2'; 'cgau3' – комплексные вейвлеты Гаусса

· 'mexh' имеет вид

Их вейвлет – спектры имеют четкие вертикальные структуры, что позволит определить экстремумы синусоиды без ошибок на масштабах 0.005÷0.1 секунд или 0.005÷0.15 секунд в зависимости от вейвлет – функции.

Для выбора оптимальной вейвлет - функции рассмотрим на рис. 2 второй модельный сигнал, состоящей из суммы синусоид с частотами 1 и 2 Гц с амплитудами 100 и нормального шума по формуле

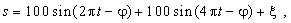
где ξ - шум с нормальным распределением и дисперсией σ2 = 1.

На масштабах меньше 0.05 секунд вейвлет – спектров, построенных с помощью гауссовых вейвлетов больше первого порядка (gaus2 – gaus4 и cgau2 – cgau3), видны множества особенностей, говорящих о том, что они чувствительны к шумам с таким уровнем. И это делает их не подходящими для использования при анализе малоамплитудных сегментов сигнала, где отношение шум/сигнал будет больше.

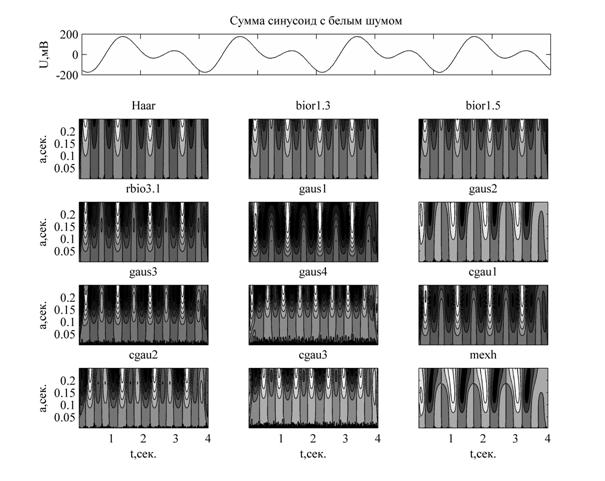
Рис. 2. Вейвлет – спектры суммы синусоид с шумом

Было предложено для дальнейшего исследования выбрать из остальных три простейших вейвлет – функции: вейвлет Хаара и два гауссовых вейвлета первого порядка, так как остальные вейвлет – функции не имеют явных преимуществ, но имеют более сложные аналитические виды и созданы для других целей ^[4].

Выбранные три вейвлет – функций были использованы для анализа вейвлет – спектров пульсограммы практически здорового человека (рис. 3.). Видно, что вейвлет – спектр с вейвлетом Хаара имеет вертикальную структуру, позволяющую определять структуру пульсового сигнала на большем количестве масштабов. В то же время, на вейвлет – спектрах с вейвлетами gaus1 и cgau1 структуры визуально очень похожи и имеют нулевые значения непараллельные оси масштаба.

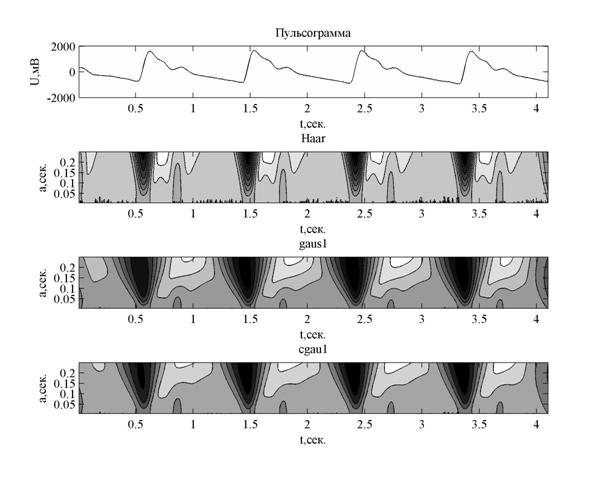
Рис. 3. Вейвлет – спектры пульсового сигнала

АНАЛИЗ ВЕЙВЛЕТ-КОЭФФИЦИЕНТОВ НА ОТДЕЛЬНЫХ МАСШТАБАХ

На вейвлет - спектрах невозможно оценить точность нахождения и количество масштабов, на которых эти точки находятся с минимальной погрешностью, поэтому были проанализированы вейвлет - коэффициенты на отдельных масштабах.

Рассмотрим подробнее вейвлет – коэффициенты на единичной волне пульсового сигнала. На рис. 4 представлена единичная волна пульсового сигнала с графиками вейвлет-коэффициентов для вейвлета Хаара и двух вейвлетов Гаусса. Вейвлет-коэффициенты даны для десяти масштабов от 0.005 (линия 1) до 0.05 секунд (линия 10), и значения вейвлет-коэффициентов растут с их увеличением.

Видно, что точки экстремумов сигнала определяются нулевыми значениями вейвлет – коэффициентов, также как и на производной сигнала. Таким образом, можно определять точки экстремума на сигнале с помощью нулевых точек на разных масштабах вейвлет-спектра.

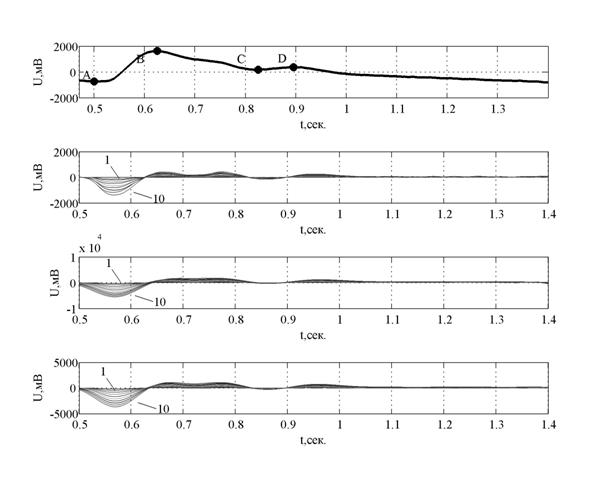
Рис. 4. Вейвлет – коэффициенты единичной волны пульсового сигнала на масштабах от 0.005(линия 1) до 0.05 секунд (линия 10) для вейвлета Хаара, вейвлета Гаусса и комплексного вейвлета Гаусса (сверху вниз).

На рис. 5 показаны графики вейвлет-коэффициентов для трех функций возле точки А - максимума пульсового сигнала t= 0.625 сек. Графики даны с точностью в один шаг дискретизации равного 0,005 сек. Видно, что при использовании функции Хаара нулевые точки вейвлет-коэффициентов, которые определяют точку экстремума пульсового сигнала, на всех десяти масштабах расположены возле точки А (t= 0.625 сек.) с точностью меньше одного шага дискретизации. В то время вейвлет-коэффициенты, найденные на основе функции Гаусса, имеют нулевые значения, отклоняющиеся от точки А (t= 0.625 сек.) при увеличении масштаба, что будет приводить к увеличению погрешности определения точки экстремума исходного сигнала.

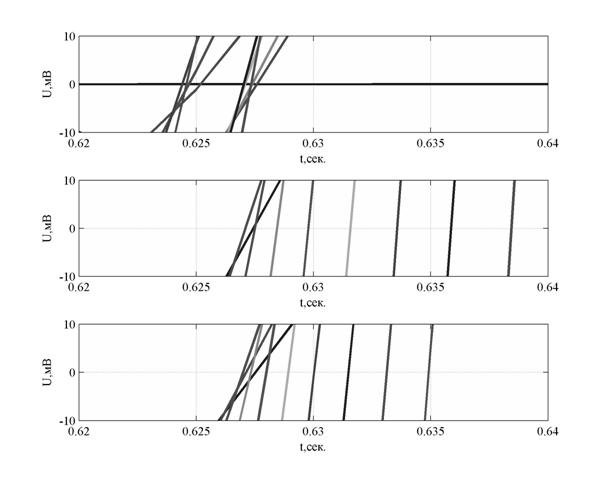
Рис. 5. Вейвлет – коэффициенты на масштабах от 0.005 до 0.05 секунд для вейвлета Хаара, вейвлета Гаусса и комплексного вейвлета Гаусса (сверху вниз) в районе точки максимума t=0.625 сек.

Определив подходящую функцию, оценим погрешность нахождения точек A,B,C,D для всех вейвлетов. Для них имеет смысл оценивать погрешность нахождения точки экстремума с помощью нулевых вейвлет-коэффициентов, начиная с масштаба больше 0.005 сек., так как вид функции не позволяет оценивать первый масштаб. Для остальных девяти масштабов вычислим погрешность по формуле:

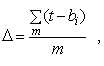
где m-количество масштабов, t- истинное положение точек экстремумов, bi - положение точек, найденных с помощью нулевых вейвлет-коэффициентов на масштабе i.

Таким образом, вычислим среднюю погрешность нахождения точек экстремумов на девяти масштабах по отдельности для каждой точки (A,B,C,D) и для каждого вейвлета, которые даны в таблице 1.

Таблица 1

Как видно из таблицы средняя погрешность для вейвлет Хаара меньше 0.005 сек. – одного шага дискретизации по времени, что говорит о достаточной корректности передачи положений точек экстремума с помощью нулевых вейвлет-коэффициентов на всех девяти масштабах вейвлет-образа. Для вейвлета Гаусса погрешность для точек A, B, Cбольше шага дискретизации, а для комплексного вейвлета Гаусса погрешность в точках B, C чуть меньше шага дискретизации. Такие погрешности не позволяют корректно определять точки экстремума даже при отсутствии шумов.

Таким образом, данное исследование позволяет выбрать вейвлет Хаара для анализа локальных особенностей пульсового сигнала, и использовать данное вейвлет – преобразование для нахождения информативных точек (экстремумов) пульсовой волны.

ВЫВОДЫ

В предложенной методике показывается алгоритм анализа непрерывных вейвлет-спектров с разными вейвлет-функциями с целью оценки их пригодности для поиска экстремумов. Важным моментом в данной методики является переход с визуального анализа трехмерных вейвлет-спектров к количественному анализу двухмерных вейвлет-коэффициентов на разных масштабах. Такой переход показывает, как работает вейвлет-анализ внутри трехмерных вейвлет-спектров (анализируемых в основном визуально) и позволяет автоматизировать анализ сигналов. Это же позволяет уже численно оценить точность нахождения экстремумов при использовании конкретного вейвлета. В результате показано, что в задаче поиска экстремумов сигнала с помощью непрерывного вейвлет-анализа наиболее точным является вейвлет Хаара.

Данную методику выбора базиса можно использовать в задачах, где возможна приемлемая количественная оценка точности работы непрерывного вейвлет-преобразования. Это позволит анализировать трехмерные вейвлет-спектры не только качественно (визуально), но и количественно.